コレクション 正四 角錐 体積 138763

1

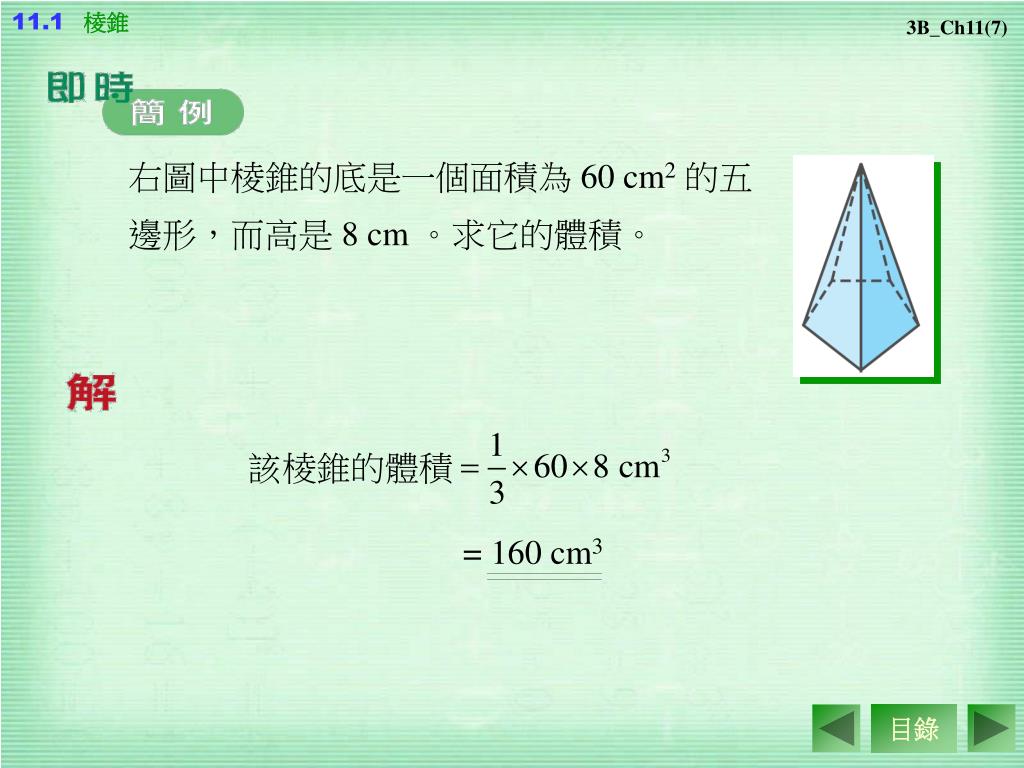
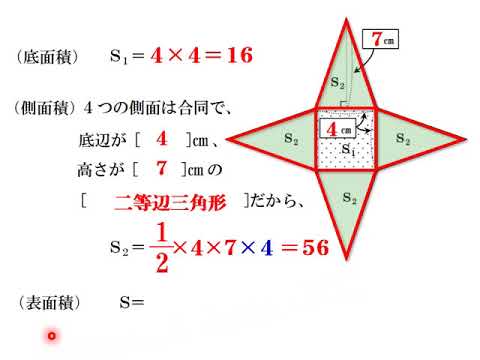
 錐体（円錐、角錐）の体積は、底面積が S S 、高さが h h の錐体の体積 V V は以下の式で表します。 V = 1 3Sh V = 1 3 S h この公式を学習したときに 1 3 1 3 になる理由は知らなかったと思います。 これは特殊な四角錐の場合には比を用いて簡単に証明することが問題 右の図の正四角錐の体積と表面積を求めよ。 解 体積 1 3 ×102× 12＝400 （cm3） 表面積底面積は 100 cm2。側面は合同な二等辺三角形だから， 1 2 ×10×13 ×4＋100＝360 （cm2） 答 体積 400 cm3，表面積 360 cm2 139 次の図の正四角錐の表面積を求めよ。

正四 角錐 体積

正四 角錐 体積-位置関係2 直線の位置関係／面と直線の位置関係／角柱・角錐の体積／立体の切断など／ 1 辺が6cm の立方体と，底面が合同で高さが等しい正四角錐正四角錐の体積（底辺と高さから） 答えを知れて良かったが、途中式が分からないので、あまり勉強にはならなかった。 a=8,h=3にすると体積がになります。 (14桁の場合) 正しくは、64です。 修正お願いいたします。 失礼致しました。 ご指摘

正四角錐の体積 底辺と高さから 高精度計算サイト

 四角錐の体積＝底面積×高さ× より 四角錐の高さ＝四角錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積＝12×12＝144（cm²）であることから 求める四角錐の高さ＝432÷144×3＝9（cm）となります。 答え 9cm ～立体の体積・表面積を求める公式 計算公式正四角錐の体積の求め方がわかる3ステップ 中3数学 中3数学2分でわかる！中点連結定理とは？？ 中1数学 文字式の分数計算問題の4つのパターン 中2数学 中学数学3つのサイコロの確率の求め方がわかる3ステップ・このことから、「 高さが1／2の正四角柱の体積（立方体の半分）」＝「 高さが1／2の正四角錐 3個の体積の和 」であることがわかります。 ・四角形は2つの三角形にわけられることから、三角形についても同様のことが成り立ち、一般の多角形についても

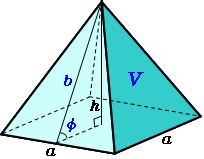
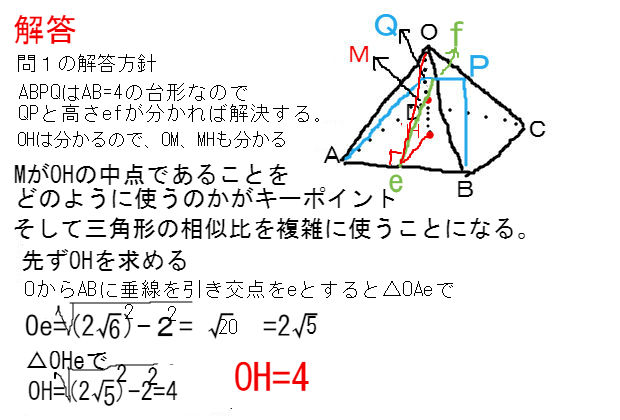
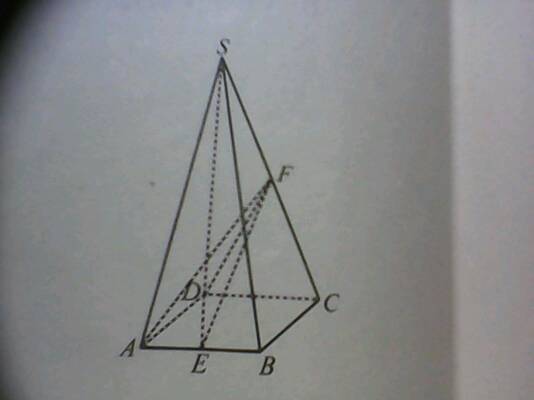
 で、左の正四角錐はこれを6で割ったものですので、正四角錐の体積は\(\frac{ 4 }{ 3 }h^3\)になりますね。 ということは、正四面体の体積は底面と高さの積を何倍すればいいのでしょう？ (？倍すればいいと考えます) 底面は一辺\(2h\)の正方形、高さは\(h\)ですの問題の立体を各方向から見ると下記のようになっています。 そこで、平面ABDで切った断面をCのほうから見たものを図1、 また、平面ACEで立体を2分割したものを図2とします。 Cを通りDAに平行に引いた直線とBRの交点をS、およびRからACに下ろした垂線の足をHとします。要点四角錐，三角錐，円錐の体積 三角錐，四角錐，円錐の体積 V は，それがちょうど入る四角柱，三角柱，円柱の体積の です． 特に，円錐については，底面の半径が r であるとき，底面積が S=πr 2 と書けるから と書くこともできます．

正四 角錐 体積のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア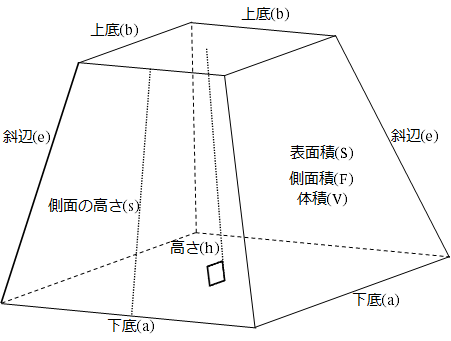
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	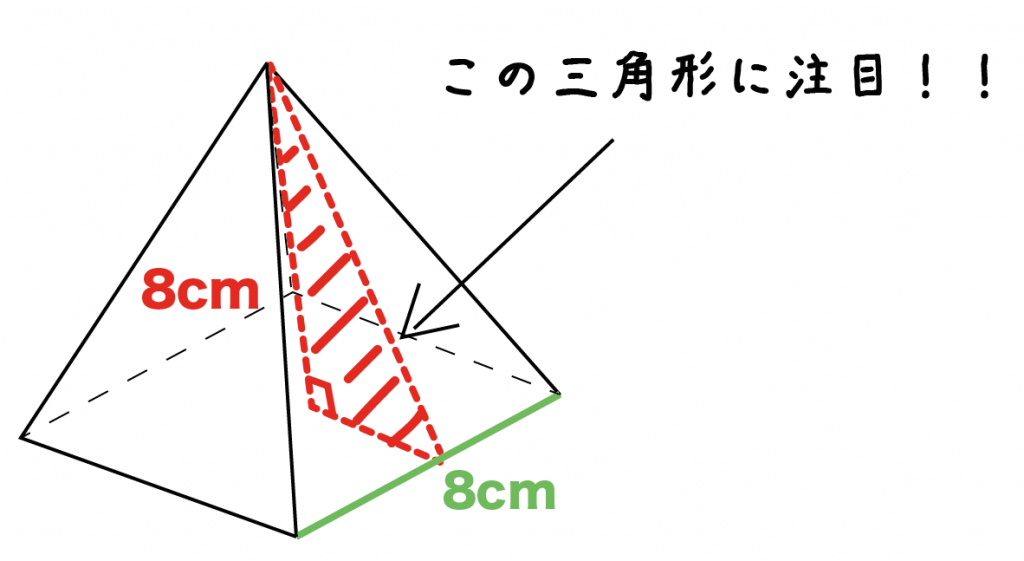エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	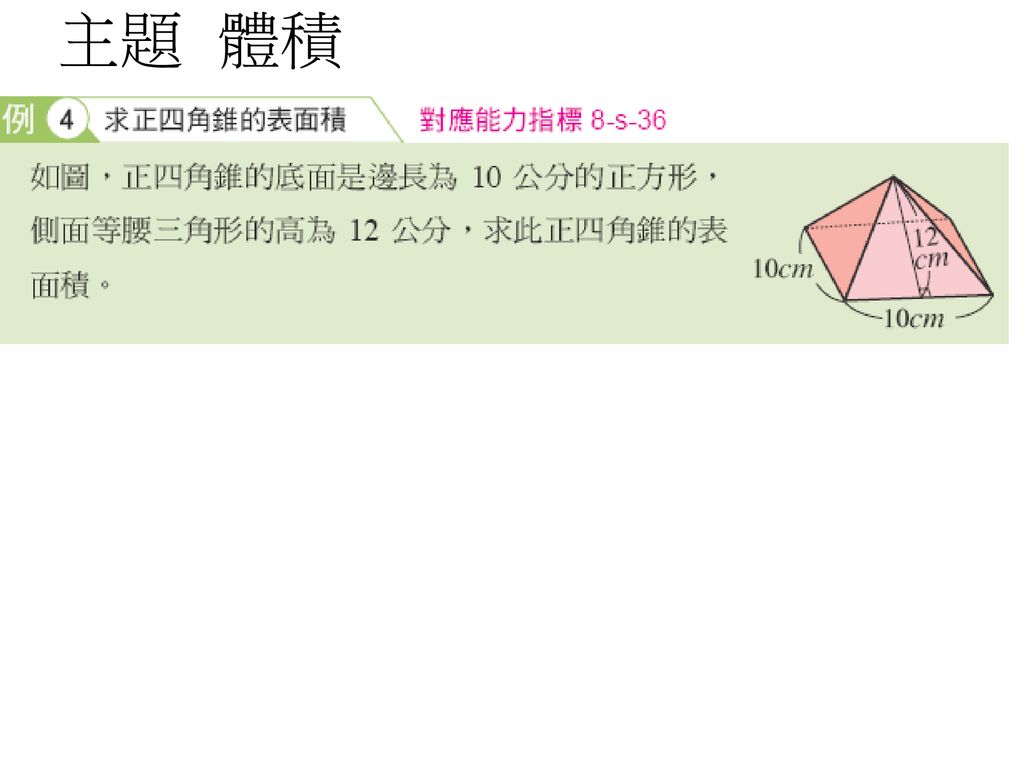エレガント四角錐表面積公式 最高のカラーリングのアイデア
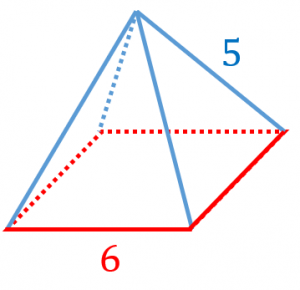エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	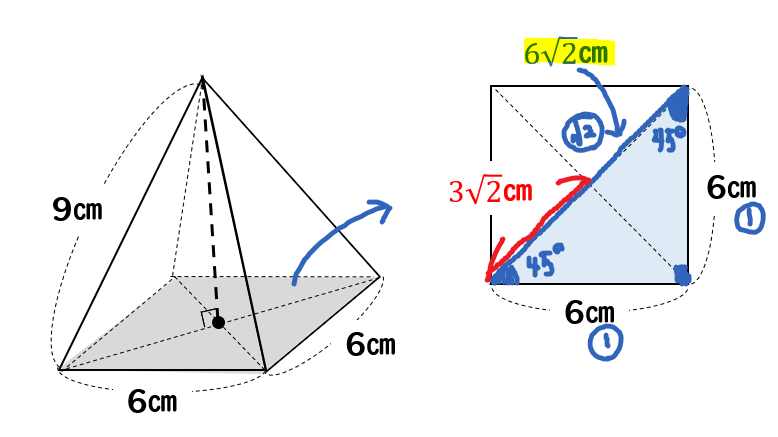エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア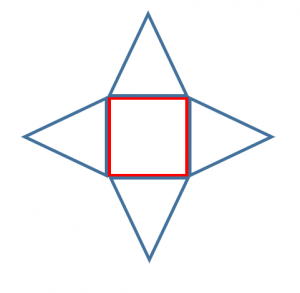
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	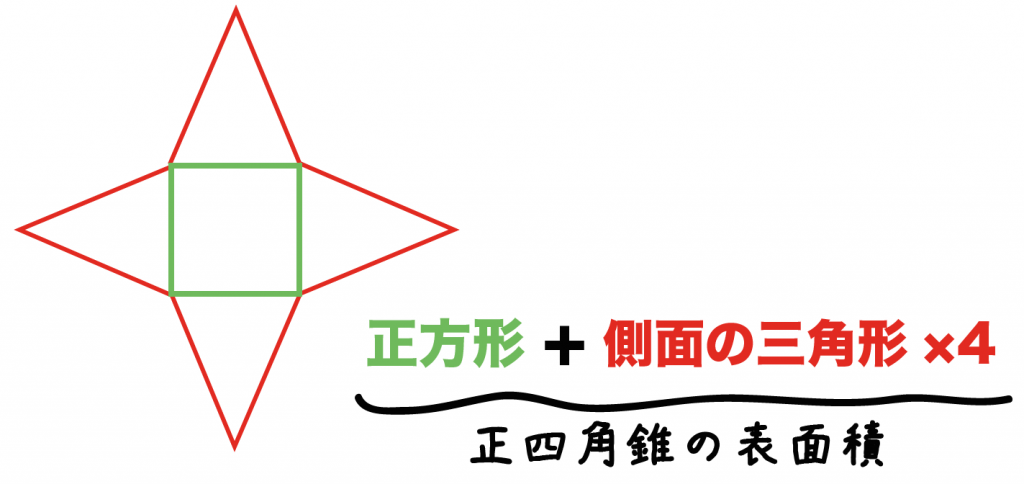エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア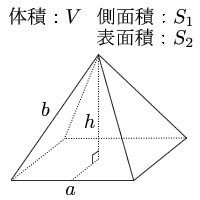
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	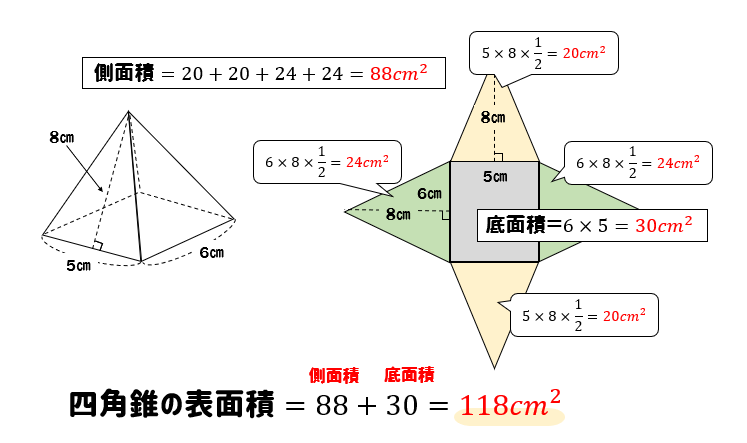エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	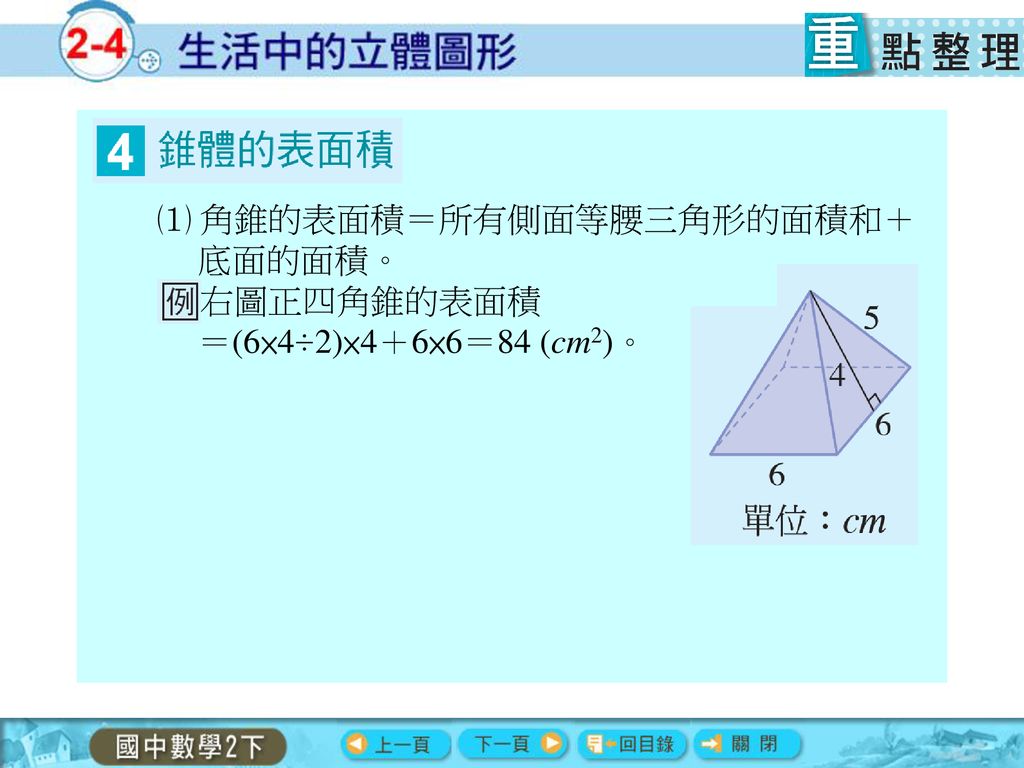エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア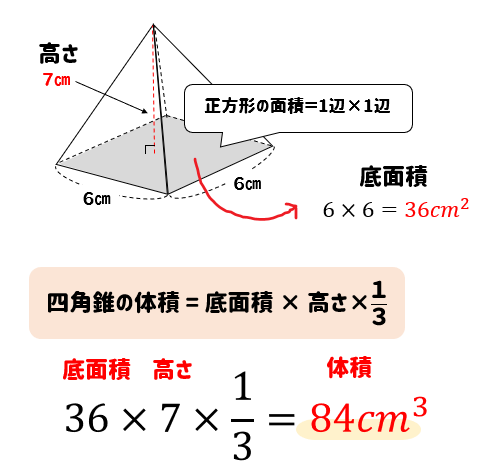
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア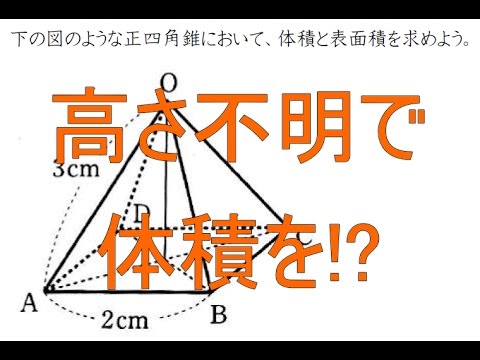
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	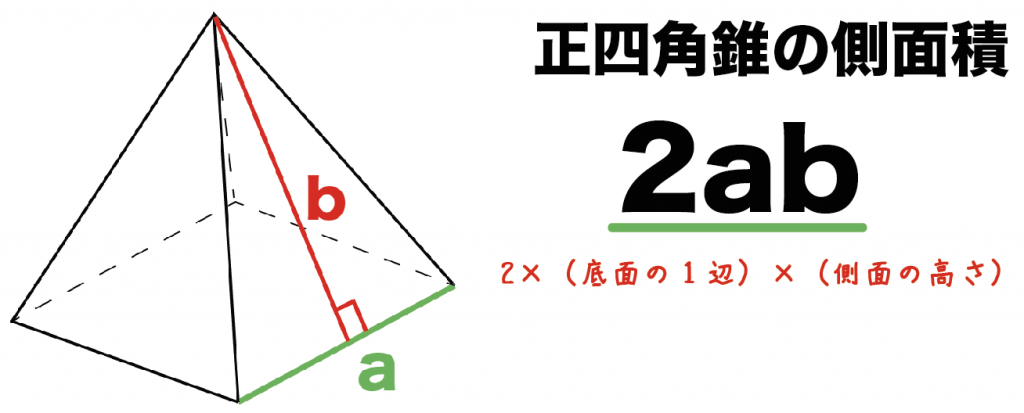エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア	エレガント四角錐表面積公式 最高のカラーリングのアイデア
エレガント四角錐表面積公式 最高のカラーリングのアイデア	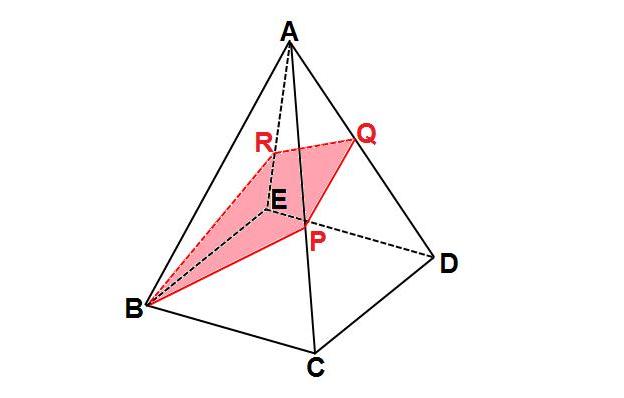エレガント四角錐表面積公式 最高のカラーリングのアイデア

 円錐の体積 下のような底面積の半径が6cm、母線の長さが9cmの円錐の体積を求めます。 色のついた部分の直角三角形を考えて高さhを三平方の定理から求めます。 h 2 =9 2 ー6 2 h 2 =45 h=3√5 体積＝6 2 円すいの体積の公式 底面積×高さ×1/3 正四角錐の体積 底辺四角錐の体積を求めるときに気をつけたいのは、 必ず\(\frac{1}{3}\)を掛ける ことです。 四角錐、円錐など、てっぺんがとんがっている錐体と呼ばれる立体の体積は必ず\(\frac{1}{3}\)を掛けてください。 よって、計算は次のようになります。