Exercises In Exercises 1 Through 14 Some Of The D Gauthmath
Simple and best practice solution for y^2(1x^2)dxx(x^2y2xy)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it Solve x^2d^2y/dx^2 xdy/dx y = (logx)sin(logx), x > 0 ← Prev Question Next Question → 1 vote 6k views asked in Mathematics by Nakul (702k points) Solve x 2 d 2 y/dx 2 xdy/dx y = (logx)sin(logx), x > 0 differential equations;
X 2 y 2 1 dx x x-2y dy 0
X 2 y 2 1 dx x x-2y dy 0-Answer and Explanation 1 Become a Studycom member to unlock this answer!Simple and best practice solution for (1x^2y^2x^2y^2)dy=y^2dx equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it
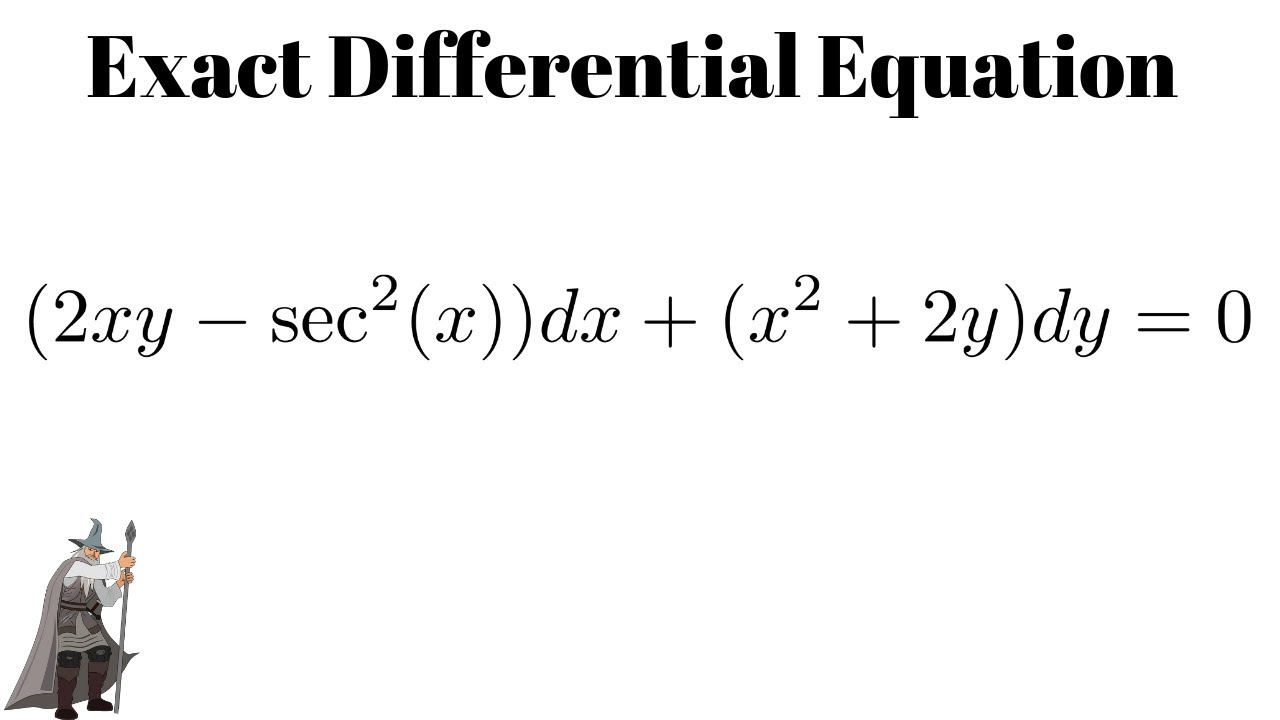
Exact Differential Equation 2xy Sec 2 X Dx X 2 2y Dy 0 Youtube
Welcome back and 3 others joined a min ago Continue with Google Continue with email 0 15k views Solve ( x 2 y − 2 x y 2) d x − ( x 3 − 3 x 2 y) d y = 0 written 38 years ago by smitapn612 ♦ 100 modified 19 months ago by sanketshingote ♦ 7Separabledifferentialequationcalculator x\frac{dy}{dx}=y^{2} en Related Symbolab blog posts Advanced Math Solutions – Ordinary Differential Equations Calculator, Bernoulli ODE Last post, we learned about separable differential equations In this post, we will learn about Bernoulli We can rearrange this Differential Equation as follows dy dx = 2x y 2y − x = 2x y 2y − x ⋅ 1 x 1 x = 2 (y x) 2( y x) −1 So Let us try a substitution, Let v = y x ⇒ y = vx Then dy dx = v x dv dx And substituting into the above DE, to eliminate y
We are asked to solve the differential equation (x − y) dy dx = x 2y We rearrange a little dy dx = x 2y x −y dy dx = 1 2(y x) 1 − (y x) (I) While I may not need to mention this, this differential equation is what is called a homogeneous differential equation I'll parang ganito po yung factor sa, vx (9 x^2 2vx)dx vx ( 6x vx ) dx 9v x^2dx 2 v^2 x^2dx 6vx^2 dx v^2x^2dx (3x^2dv v^2 x^2dx)Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing
X 2 y 2 1 dx x x-2y dy 0のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 | ||
「X 2 y 2 1 dx x x-2y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
「X 2 y 2 1 dx x x-2y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「X 2 y 2 1 dx x x-2y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 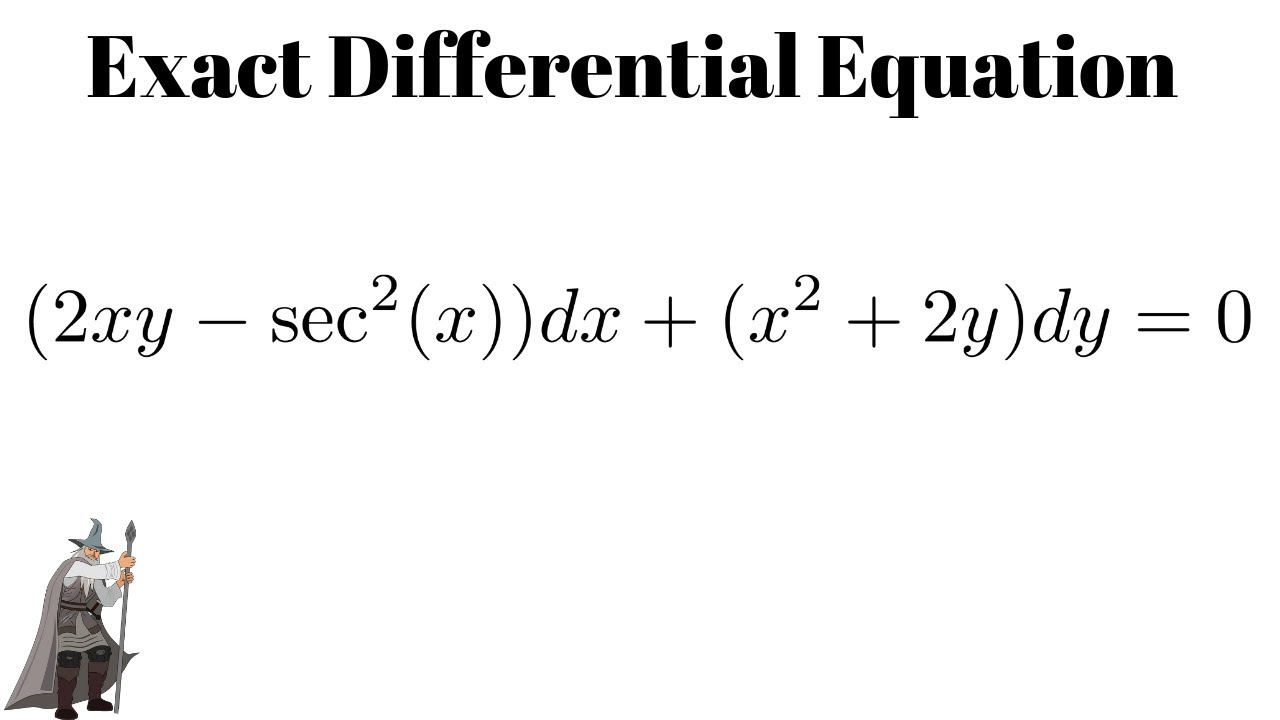 |  |
 | ||
「X 2 y 2 1 dx x x-2y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「X 2 y 2 1 dx x x-2y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
「X 2 y 2 1 dx x x-2y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「X 2 y 2 1 dx x x-2y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「X 2 y 2 1 dx x x-2y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「X 2 y 2 1 dx x x-2y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「X 2 y 2 1 dx x x-2y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「X 2 y 2 1 dx x x-2y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
(x 2) 2 y(x 2)dy/dx y 2 = 0 Substituting x 2 = t, we get dx/dy = dt/dy which passes through the point (1, 3) Therefore, from Eq (1), we get That is, the solution curve intersects y = (x 2) exactly at one point and not at two points Therefore, option (A) is correct and option (B) is incorrect Checking for option , we Given x^23xyy^2=0 Differentiate each term with respect to x (d(x^2))/dx (3d(xy))/dx (d(y^2))/dx=(d(0))/dx Use the power rule, dy/dx = nx^(x1), on the first
Incoming Term: x 2 y 2 1 dx x x-2y dy 0, x 2 y 2 1 dx x x-2y dy 0 non exact,




0 件のコメント:
コメントを投稿